Calibration labs typically use deadweight testers as their primary standard. The weights used to produce the pressure in these devices are suspended or “floating” over the medium under the piston and weights. These weights are also buoyed within the ambient air. This upward buoyancy force must be subtracted from the downward force exerted by the weights to most precisely determine the pressure produced by deadweight masses. The density of the ambient air and local gravity is also factored into a mass’s buoyancy.

What is Buoyancy?
Buoyancy is the ability or tendency of a mass to float in a medium, specifically gas or liquid. Archimedes’ principle states any body completely or partially submerged in a fluid at rest is acted upward upon by a buoyant force. The magnitude of the buoyant force is equal to the weight of the fluid displaced, as shown below:
Fb=ρgV
Where Fb is the buoyancy force, V is the volume of the object, ρ is the density of the fluid, and g is the gravitational acceleration.
The buoyant force around a deadweight tester's weight and piston system must be accounted for in a calibration setting. Air buoyancy can cause an error as high as 0.015% of the indicated value. This level of buoyancy error can be significant when calibrating instruments with strict parameters, especially high accuracy or low pressure devices.
In static fluid or air, buoyancy can be determined by the pressure exerted on either side of an object, upward and downward. In the case of a deadweight tester, this force would be atmospheric pressure.
Measuring pressure in pounds per square inch isn’t just for fun. The weight of the fluid displaced by the object will equal the buoyant force of the object, i.e. its buoyancy. This force acts upon the entire object. For example, if the atmospheric pressure 14.5 psi, then 14.5 pounds of pressure is being applied to every single square inch of that object’s surface. Hence, as the pounds per square inch of pressure rises so will the object’s ability to “float.”
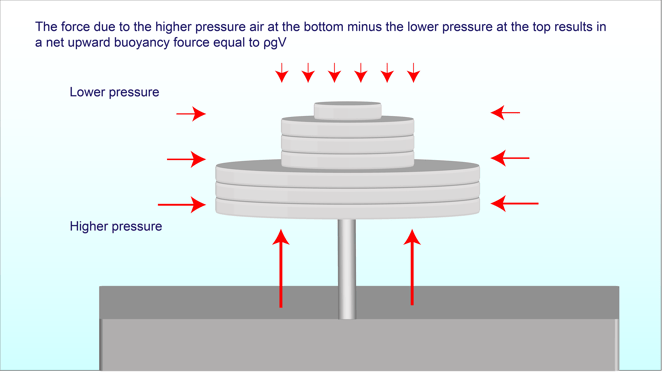
This external force must be accounted for to ensure the highest accuracy possible. Any mass will need to have an air buoyancy correction based on the following formula:
Air buoyancy correction = (1-ρa/ρm)mt
Where mt is the true mass of the deadweight used, ρa is the density of the air (kg/m3), and ρm is the density of the masses (kg/m3).
This correction is only required for gauge calibrations where ambient air surrounds the weights and not for absolute calibrations where the weights are in a vacuum under a bell jar. The buoyancy effect is negligible in absolute/vacuum calibrations because the ambient air has been removed.
Buoyancy is the reason ships stay afloat and hot air balloons rise in the atmosphere. In calibration labs, buoyancy's effects are not so apparent but it still acts upon all objects and must be corrected to guarantee the most accurate pressure calibrations.
Related Reading:



