Flow meters come in many types: some measure the volume of liquid or gas flowing in a pipe (volumetric flow meter); some measure the mass flowing in a pipe (mass flow meter).
Mass flow is measured in units of mass per unit time, using pounds or kilograms per second. Volumetric flow is measured in volume per unit time, in units like gallons or liters per second. The relationship between volumetric and mass flow in a pipe becomes apparent when looking at the equation used to calculate each:
Q = A * v and W = ρ * Q
Where Q = the flowing volume, A = the cross-sectional area of the pipe, v = the velocity of the fluid in the pipe, W = the mass flow rate, and ρ = the fluid density.
Whether it is volumetric or mass flow, there are many different types of meters that are used for measurement. This post will concentrate on flow meters that infer their measurement from pressure: Orifice Plates, Venturi, Nozzles, and Averaging Pitot Tubes.
All derive the flow using differential pressure. Essentially, each one creates an obstruction in the flow and the difference in pressure between the upstream side of the obstruction and the downstream side is proportional to the volumetric flow. To obtain mass flow in any of these, the density of the fluid must also be known.
A Sonic Nozzle, also called the Critical Flow Venturi or Critical Flow Nozzle, is used with gas only. This type has a distinct advantage over the others due to their unique operating principle, which only requires one pressure reading to infer the flow. This may seem trivial, but when using differential pressure you either need two pressure transducers or a differential pressure transducer. Either way, there is more error associated with these as opposed to a single transducer. For this reason, sonic nozzles are used in gas flow calibrators because of their higher accuracy.
Depending on the accuracy required and the suitability of the application, one type of flow meter may be better than another. The pressure sensing element should be accurate enough to provide the level of accuracy in flow that is required and have a sufficient response rate to measure rapid changes in fluid flow. There are many other methods of measuring flow beyond the scope of this article, including Positive Displacement Meters, Turbine Meters, Coriolis Meters and Thermal Flow Meters.Some of the more prevalent flow meters using pressure or differential pressure to infer volumetric or mass flow are described below.
Orifice Plates determine flow by measuring the difference between the upstream pressure and the downstream pressure. This is usually accomplished using a differential pressure transmitter.
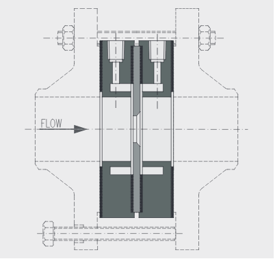
Venturi Meters take advantage of the physical properties that a restriction in a pipe will cause an increase in velocity and a reduction in pressure, according to the law of conservation of mechanical energy. This reduction in pressure is proportional to the volumetric flow rate.
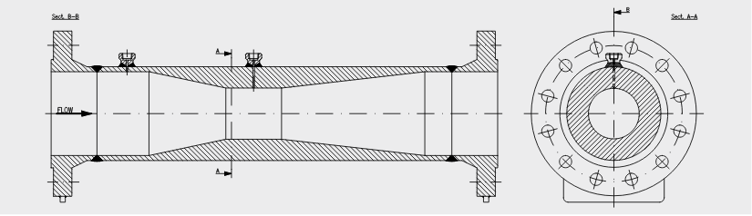
A Nozzle is similar to a Venturi but is typically designed to fit between two flanges and doesn't have a tapered exit. The same principal of differential pressure is used to infer flow rate.
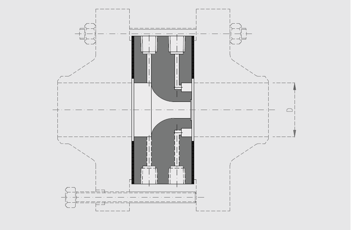
An Averaging Pitot Tube is a tube with multiple holes facing upstream and downstream. The tube has an inner wall that separates the upstream holes from the downstream holes. The tube extends across the diameter of the pipe where the flow is being measured. The upstream holes enter into a plenum where the impact pressure is averaged. A separate plenum on the downstream side averages the pressures from the downstream side of the tube. In a flowing condition, the upstream holes experience a higher pressure than the downstream holes and the difference is proportional to flow.
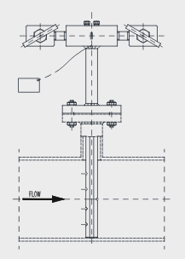
At the throat of a Sonic Nozzle, or minimum area point, the gas velocity reaches the speed of sound. At this point, gas velocity and density are maximized, and the mass flow rate is a function of the inlet pressure, inlet temperature, and the type of gas. These can achieve a higher degree of accuracy when compared to meters that require a differential pressure because they only require a single pressure measurement to infer the flow.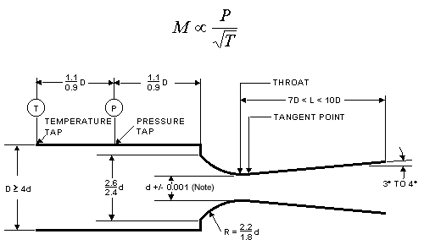
The flow rate in all these meters is derived from Bernoulli's equation, which states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure.
Where P = Pressure, ρ = Density, V = Velocity, g= Gravity, and h = height.
If the height and gravity is the system remains constant, we can simplify this equation to:
Now we can see that when the velocity increases in a restriction, the pressure must decrease.
Conclusion
Because these meters derive the flow measurement from pressure readings, the more accurate the pressure instrument, the more accurate the flow reading. Direct measurement with high accuracy pressure transmitters that match the level of accuracy required is recommended, and regular calibration of these transmitters is necessary to maintain the level of accuracy needed.


