When most people think of or talk about fluids, they usually mean liquids. This is not the complete picture. In fact, a fluid is a medium having particles that easily move and change their relative position without a separation of the mass and one that easily yields to applied forces. This means fluids include gases because they also flow. In fact, the root of the word ‘fluid’ is from the Latin ‘fluere,’ which means “to flow.”
Our present-day experiences may lead us to the conclusion that gases are compressible and liquids are incompressible. Consider the rebound felt when a tire pump handle is quickly released after compression; this demonstrates a force exerted by the air being compressed into a smaller volume. The volume re-expands to its original size when the compressing force is removed. Similarly, if we hold our finger over the small hole in a spray bottle, we immediately feel a resisting force when the pump trigger is pressed. Based on this observation, the liquid appears to be incompressible.
The following is an examination of the compressibility of fluids and solids as applied in a calibration laboratory. Understanding the behavior of these fluids under pressure is critical to a successful and accurate calibration.
First, some common terms should be defined:
- Fluid - a material that flows readily and requires a vessel to contain it.
- Gas - the state of matter that takes the shape of its container and does not have a definite volume.
- Liquid - the state of matter that takes the shape of its container and has a definite volume.
- Solid - the state of matter that holds its own shape and has a definite volume.
- Compressible - having the ability to change in density with applied pressure.
- Density - mass per unit volume.
- Chemical Bond - the transfer or sharing of the outermost electrons between two or more atoms.
- Van der Waals Force - attractive forces between all molecules, caused by the fluctuating polarizations of nearby particles, and which only becomes significant if the molecules are very close together.
How do gases behave differently than liquids?
Gases behave differently than liquids. Why? To understand what is happening at the macro level, we need to understand the inner workings within the material at the atomic and molecular levels. Within any substance, the chemical bonds, polarity, forces, plus the physical configuration of the atoms in a molecule determine the gross material properties, such as viscosity and compressibility. These forces, acting at an atomic scale, are the main contributors to the properties we experience in these bulk materials.
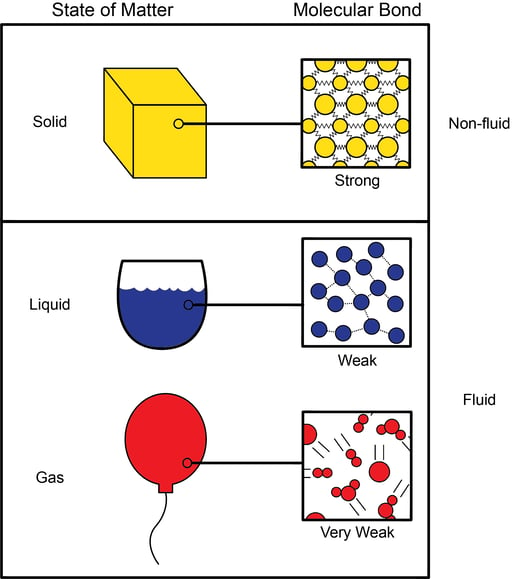Figure 1. States of Matter with Bonds in Each State
In Figure 1, a comparison of the three common states of matter, solid, liquid, and gas, shows the types of bonding within each state. In each illustration, we see a very small volume of a material magnified and a simplified representation of the respective bonds within the material. Below is a more detailed explanation of the different states with references to the illustrations.
Solids
Solids hold their own shape because the chemical bond, shown as springs between each atom, is relatively strong. However, the like charges of the electrons act to repel the atoms as they get closer together. Conversely, if the atoms move apart, they are pulled back toward each other by the bond. The distance between each atom is very small due to the strength of the bond, but this bond can only hold them together so tight because of the repelling forces. So when a force is applied to this cube from every direction, the resistance to compression between each atom is very high, this results in minimal compression in the bulk solid.
Liquids
Liquids, on the other hand, have more space between the molecules, allowing them to have more relative motion. However, the intermolecular bonds aren’t quite as strong as in solids. Water, for instance, is a polar molecule and exhibits dipole-dipole attraction, as shown by the dotted lines in Figure 1. The oxygen atom is slightly negative and the two hydrogen atoms are slightly positive. Since these dipole charges are much lower in strength than typical bonds, the Van der Waals forces between molecules are weak and are not constant. Each one may break and be remade many billions of times per second. This is what allows water to flow and yet remain a liquid. The weaker intermolecular forces and higher intermolecular spacing is the reason liquids can be compressed more than solids.
Gases
For gases such as nitrogen or air, there are no bonds between molecules at normal temperatures and pressures. Each molecule is moving at a high rate of velocity in various directions. When two gas molecules collide, they rebound off each other with perfect elasticity. There are no losses in the collisions. The intermolecular spacing is too large for intermolecular forces to be significant. At room temperature and standard pressure, the average distance between gas molecules is about ten times the diameter of the molecules themselves. So when an external force is applied to gas molecules, they are forced closer together making gases highly compressible.
Rate of Compressibility
Now that we know at a molecular level that gases & liquids are more compressible than solids. What about the compressibility of common pressure media used in a calibration laboratory? The relative amount of compressibility of a material with an applied force determines our perception of stiffness. When a material is compressed from all sides, it will shrink proportionately to the applied pressure. The proportionality constant is called the Bulk Modulus.
Β = - V * (∂P ⁄ ∂V)
Where B = Bulk Modulus
V = initial volume
∂P/∂V = Change in pressure with respect to the change in volume
Notice that an increase in pressure causes a decrease in volume, this implies that the density of the material is being increased. If the same force is applied to an equal volume of a solid, a liquid, and a gas, the relative amounts of volume reduction become evident. The isothermal bulk modulus of each state of matter may be compared to obtain an order of magnitude ratio. Below is the bulk modulus for some common materials in each state:
Stainless Steel: -23,600,000 lbf./sq. in.
Water: -310,000 lbf./sq. in.
Air, at STP: -14.7 lbf./sq. In.
A comparative ratio of materials is expressed here:
Stainless Steel : Water : Air = 1,600,000 : 21,000 : 1
The numbers are the relative stiffness of the materials. The higher the number, the less compressible the material. For example, the ratio of water to air is 21,000:1, so we don’t perceive the compression of water in the spray pump with the hole blocked. It is being compressed by such a small amount that we can’t detect it with our senses.
It should be noted that bulk moduli are pressure and temperature-dependent. For water, as the pressure increases, the bulk modulus increases. As the fluid temperature is increased from 0°C at constant pressure, the bulk modulus increases, peaks at around 330,000 lbf./sq. in. at about 45°C, and then decreases.
This creates a complex chain of events in a calibration environment. In high-pressure hydraulic calibration systems like the Mensor CPC8000-H, we rely on liquid media as our pressure medium due to safety concerns. As the system pressure increases, the fluid compresses, and all of the containing components expand (pressure controller, tubing, fittings, pressure chamber, etc). Parts surrounded by fluid compress, and the bulk modulus of the medium changes with pressure and temperature. In high-pressure systems, the consideration and compensation of relative bulk moduli, driven by the material bonding, along with good engineering make calibration systems accurate and reliable.
Conclusion
The compressibility of fluids plays a critical role in the design of a process system in the industrial sector as well as maintaining efficiency in the infrastructure of a calibration lab. Selecting the proper calibrator while optimizing the system to compensate for the compressibility of the system components and the media being used will provide more accurate calibration results. Compressibility can vary greatly with different liquid fluids with differences in bulk modulus, viscosity, temperature coefficient of the media, and solubility. We will go in-depth with the comparison of compressibility in different liquid media commonly used for hydraulic calibration in part II of Compressibility of Fluids.
Related Reading:
