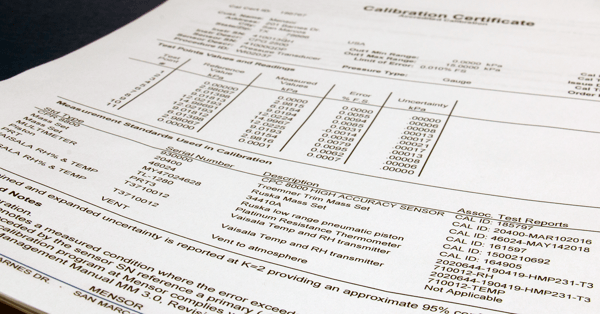
Do you ever question the accuracy and uncertainty specifications of your favorite calibrator? Maybe you've received a calibration certificate for your instrument and noticed that it mentions something like "...reported at k=2" at the bottom of the certificate? This article is dedicated to helping you understand the meaning of k=2 and how it affects the validity of a calibration.
Mensor product accuracies are reported with a coverage factor of "2." The case is the same when you receive a calibration certificate from Mensor, you will notice the following statement: “The combined and expanded uncertainty is reported at k=2 providing an approximate 95% confidence level.”
Typically, uncertainty in calibration products is reported as expanded uncertainty. Per the Guide to the Expression of Uncertainty in Measurement (GUM), the expanded uncertainty is a measure of uncertainty that defines an interval about the measurement result within which the value of the measurand can be confidently asserted to lie. The expanded uncertainty is obtained by multiplying the combined standard uncertainty by a coverage factor, k.
Here’s what this "k" means, both practically and statistically: The value of the coverage factor, k, is chosen based on the desired level of confidence to be associated with the interval defined by the expanded uncertainty.
As an example, the results data displayed on a calibration certificate will have a column labeled "Uncertainty." This is a calculation of the uncertainty - or potentially how much error there could be - in the measured values. Each of the standards used in the calibration (as listed in the "Measurement Standards Used in Calibration" section of the certificate) has uncertainty associated with their specification. A total uncertainty budget is calculated from these uncertainty values for each measurement point, and that is what is presented in this column of the certificate.
For any statistically valid data set with a normal distribution, also known as Gaussian distribution, (plotting the heights of a number of randomly selected people is a good example) will yield a bell cure. Calculating the mean and standard deviation of the data set will show that approximately 68% of the data points will lie within one standard deviation of the mean, 95% of the data points will lie within two standard deviations of the mean and 99.7% of them will lie within three standard deviations of the mean.
k=1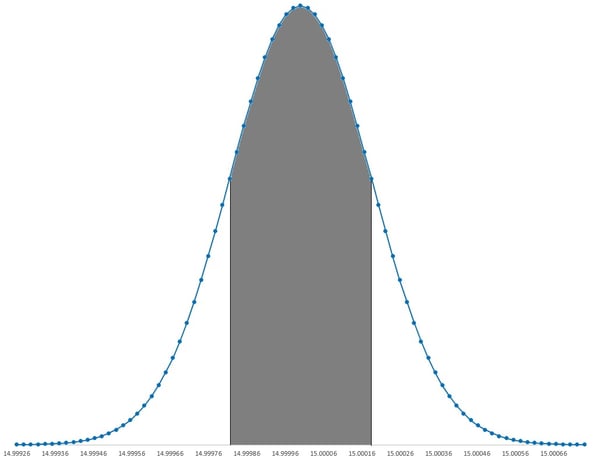
68% of data within one standard deviation of the mean
k=3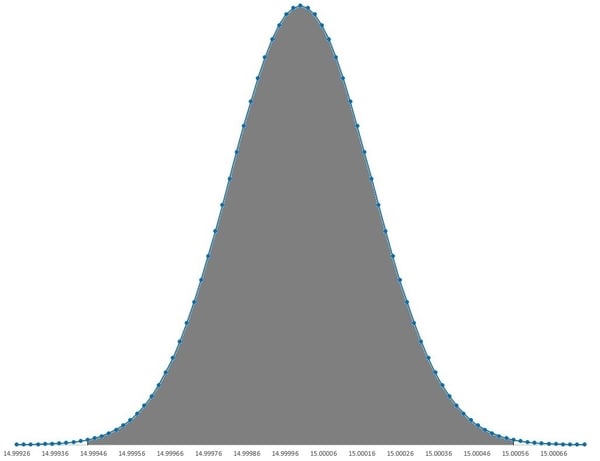
99.7% of data within three standard deviation of the mean
Calibration or measurement data yields a normal distribution curve just like this. The coverage factor, or ‘k’ value, determines the confidence in the data points within a certain standard deviation value. For k=1, there is a confidence that 68% of data points lie within one standard deviation, while k=2 means a confidence that 95% of the data points would lie within two standard deviations. Similarly, k=3 means a really high confidence value that 99.7% readings would lie within three standard deviations of the mean.
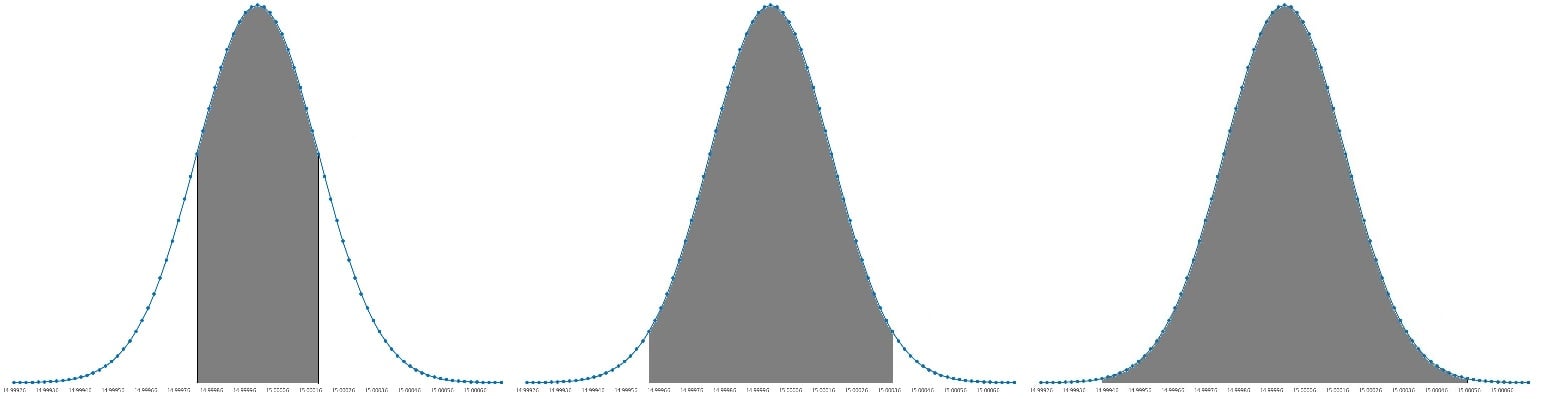
Comparison of k = 1, k = 2, and k = 3
As k=1 is not an acceptable standard for reporting uncertainty as it leaves a lot of room for passing erroneous readings. On the other end of the spectrum, k=3 really calls for an extremely narrow window for passing erroneous readings.
k=2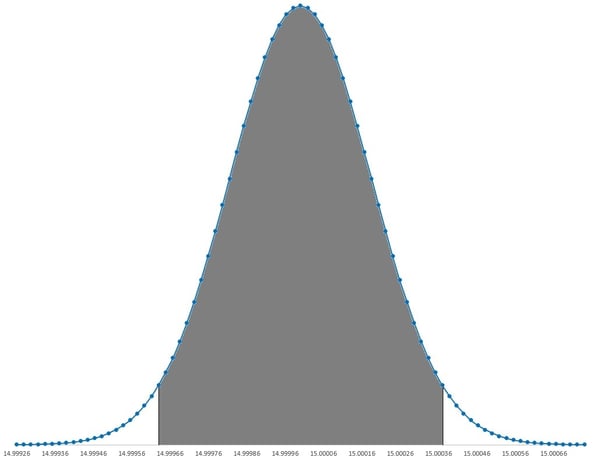
95% readings within two standard deviations of the mean
The statement of uncertainty is reported with a coverage factor of k=2, which indicates approximate 95% confidence (it's actually 95.4%). On a practical level, this means that if you were to make 100 measurements, you could be confident that (at least) 95 of them would be accurate to within the stated uncertainty.
Related Reading:
- The Fundamentals of Pressure Calibration
- How to Calibrate Pressure Instruments
- 10 Reasons to Calibrate Your Instruments
- What is the Difference Between NIST Traceable and ISO/IEC 17025 Accredited Calibrations?
- What Does As-Found and As-Left Data Mean in a Calibration?
- What is Intelliscale Accuracy? | A Mensor Measurement Specification
